“The road to success is always under construction.”
Steve Maraboli, Life, the Truth, and Being Free
In the previous article, we presented the problem of map matching, and now we'll jump into fine details of the art.
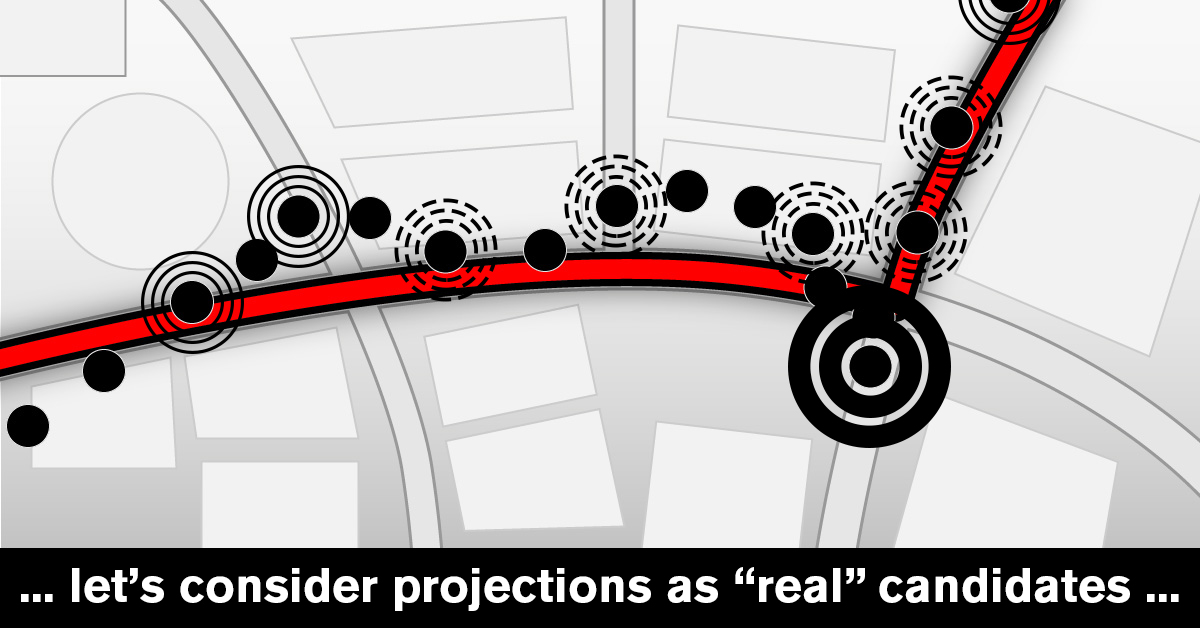
Entry to the process is a GPS position A with all additional data presented by tracking devices. Also, as we previously learnt, GPS positions can be off (and usually are, at least a little), so we need to address that first. We take projections of the position to the all nearby roads and intersections and consider them candidates for the actual (real-life) position.
To be able to do it efficiently, we use Mireo's digitalized map and query it for all such items in some radius around the original point. Mireo's digitalized map is organized in a way that such query is very fast, and now we have our set of candidates. Naturally, the larger the radius, the longer this operation takes. This scales with quadratic growth in respect to the radius itself (because we are searching in the whole area of a circle, of course). A good rule of thumb is to set this radius around 30-50 meters. In some rare cases, this was not big enough, so we decided to adjust it in some situations - when the HDOP of the position is just good enough to be accepted, we increase the radius a bit. That makes the computational process slower, but experience shows that this situation is rather rare, and being able to match such positions is quite beneficial for the whole system. Nobody likes a "hole" in their matched path.
In a busy town, there can be many such projections – up to twenty or more. Of course, only one of them will be output as a result of this process. The next step is to grade them. For each candidate, we calculate two components:
- direction score how aligned the projected position is in respect to original position's direction (most GPS devices send the info in which direction the vehicle is moving). The bigger the angle between them, the smaller the score. For example, if the original position faced north, it's less likely that the actual position should face east.
- distance score how far the position is from the reported position. The closer it is, the better the score.
Out of all the candidates, we pick the five best to continue the process. We can call this set Ac.
One of Mireo's core products is navigation software, and its integral part is a routing algorithm. The specialized version that works extremely fast for short routes, which we call local router, is used for the next step. All five (there might be less, but in most cases it's five) candidates from the original point (Ac), as well as the candidates from the previous point (Bc) are the input to the many-to-many routing algorithm in local router. This algorithm finds the best (1) route from all candidates in Bc to all candidates in Ac, and effectively uses the knowledge that all points are relatively nearby, reusing all the data it can, which is a huge improvement compared to executing the routing algorithm up to 25 times.
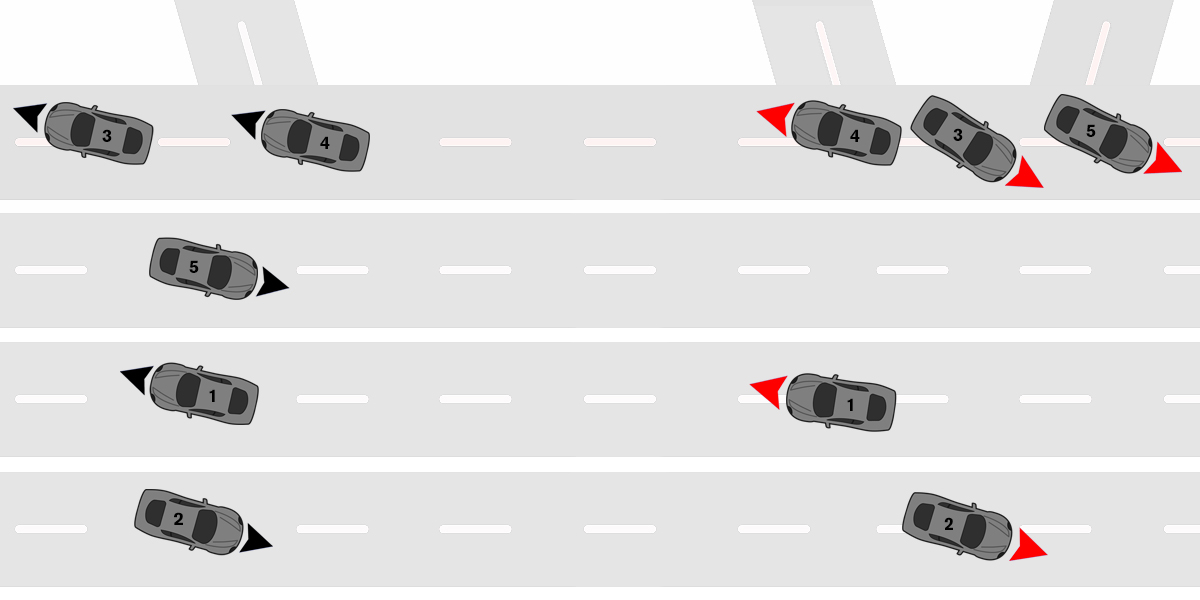
Two sets of candidates - Red (Ac) and Black (Bc), points in each set are sorted by score
Knowing all the routes between all the points helps with the next step in which we select the best candidate in Ac for which candidate in Bc, using the previous scores with an additional component:
- path score how well does the candidate fit in path reconstruction taking the distance between points, road distance and vehicle's reported speed into account. For example, if the average speed between two original points was 20 meters per second, and the difference in timestamps is 5 seconds, we'd prefer to match candidates that are 100 meters apart.
In this case, some of the points from either Ac or Bc can be eliminated - if they have no favorable predecessor or successor, they are removed from the corresponding set. This way, we build up a network of connected points and possible paths that the vehicle actually took.
This process can go on for a while (consider a case of two parallel roads with GPS signal being low), but it eventually ends in one of the cases:
- either one of sets (Ac, Bc) has a single point, we consider it a root
- the chain of points is too long, thus we select the best candidate to be a root.
When we establish a root point, we traverse backwards through the chain of candidates and select the best one in respect to the root. Again, consider two parallel roads R1 and R2; when a root is selected from the road R1 traversing backwards will select all the candidates from the same road. At this moment, we can't change our mind about the candidates anymore, and it's time to output them further into the system.
There are still some things to consider, however. In practice, the biggest problem can lay in imprecision of devices or being tied to granularity of a second. Most devices send the time between points as an integer representing number of seconds since epoch, rounding the value in the process. It's intuitive that it's in one's best interest to receive the data from the device as often as possible, but it may not always be right. Consider a point P1 happening in T1 = 0.9s (2), and P2 happening in T2 = 2.0s. The difference between those points is 1.1 seconds. But, if we truncate the times to integers, as it's often the case, the difference increases to 2 seconds, which is almost double! (3) For such small distances (which is in about 20-60 meters in this case), this makes a huge difference. For that reason, as we strive to be correct in all our math, some points that are valid can not be connected to the previous ones. In this case, our algorithm has an additional condition in which it can decide to ignore a point or two if there is a burst of points in a small period of time. There will be no loss in deciding what the actual path was, anyway. We can be honest here - there is no practical gain if vehicle sends data every single second because it won't change it's course, road or route more than once in a couple of seconds. Therefore, we consider the best practice to be for the device to send the data every 3-5 seconds or every 100 traveled meters.
There are other kinds of matching problems that can occur, of course. Some of them being:
- vehicle moving, but not driving (for example, on a ferry or a tow truck)
- vehicle moving, but there is no GPS data (tunnels)
- vehicle reports "obviously" incorrect data, but it can mathematically connect to previous points (this often happens as vehicle leaves a tunnel or exits an underground garage)
In those, and some other specific cases, we need to adapt our strategy further. We can "patch" long gaps with another call to the routing algorithm, but in this case, it's our long distance router instead of local router. Unlike local router, long distance router can connect points between different countries and there is virtually no limit how far apart the points can be. When there is a big gap of data missing, we have a lot of room for guessing the probable route, and there almost are no constraints in creating a sensible one (for example, vehicle can accelerate, decelerate and stop several times to accommodate start and end times).
And that's a wrap! We hope you enjoyed reading about Mireo's map matching process, and learned something new while doing so.
- What's best? Shortest, fastest, balance of both? Will it make a difference for such short distances?
- Time represented as a difference between real time and some fixed time point, to simplify the math instead of writing "October 2nd, 2020 at 12:34:56".
- Truncating 0.9 to an integer gives 0, thus 2 - 0 = 2.